LLMs Can’t Understand Time — At Least Not Naturally
Why (and what actually works), explained across 3 acts
This is a special post in AI Realist newsletter. It is opening a series of posts by guest authors who have an exceptional expertise in the area of AI. Today’s post is by
, an expert in time series & networks, responsible AI and AI for the financial sector. He has an impressive publication record in top conferences such as ACL etc.Subscribe to Gary’s newsletter “Quaintitative“ for additional insights on AI:
My realist take (since this is a guest post on AI Realist) on LLMs for time series.
When LLMs first became accessible and popular in 2022, one easy way to tell if someone was selling snakeoil was if they claimed that either ChatGPT or LLMs could forecast or predict something in the future.
You could discount everything they said after that.
Someone who said that obviously did not understand how LLMs then worked, and were essentially hallucinating or bullshitting with great confidence.
LLMs are trained on text data. To forecast, you are working in the domain of time series data.
Things have evolved since. I would listen more patiently now for the details if someone said he or she used LLMs for forecasting due to shifts in the field. However, there is still a clear distinction between LLMs for language or text, compared to time series foundational models inspired by LLMs.
Let me explain this. In 3 short acts.
Act I: The Classical World of Time Series Modelling
For decades, way before neural networks were practically usable, forecasting or predictions with time series data was the domain of statisticians and econometricians. Time series data is fundamentally different from tabular, image or text data. You can shuffle rows in tables, mix up images, or rephrase text, and the meaning would still be largely intact.
So we come to the first fundamental property of time series - sequence. Mixing up the sequential order of time series data renders it meaningless.
This is the world of models like ARIMA. Understanding such models provides a clear understanding of what matters for time series data.
The AutoRegressive Integrated Moving Average (ARIMA) models and its variants dominated time series analysis for ages. They captured the essential insights needed to analyse or make predictions with time series data.
The core ideas:
AutoRegressive (AR): Current values depend on previous values
Integrated (I): Many series become predictable after differencing
Moving Average (MA): Current values depend on errors of previous predictions
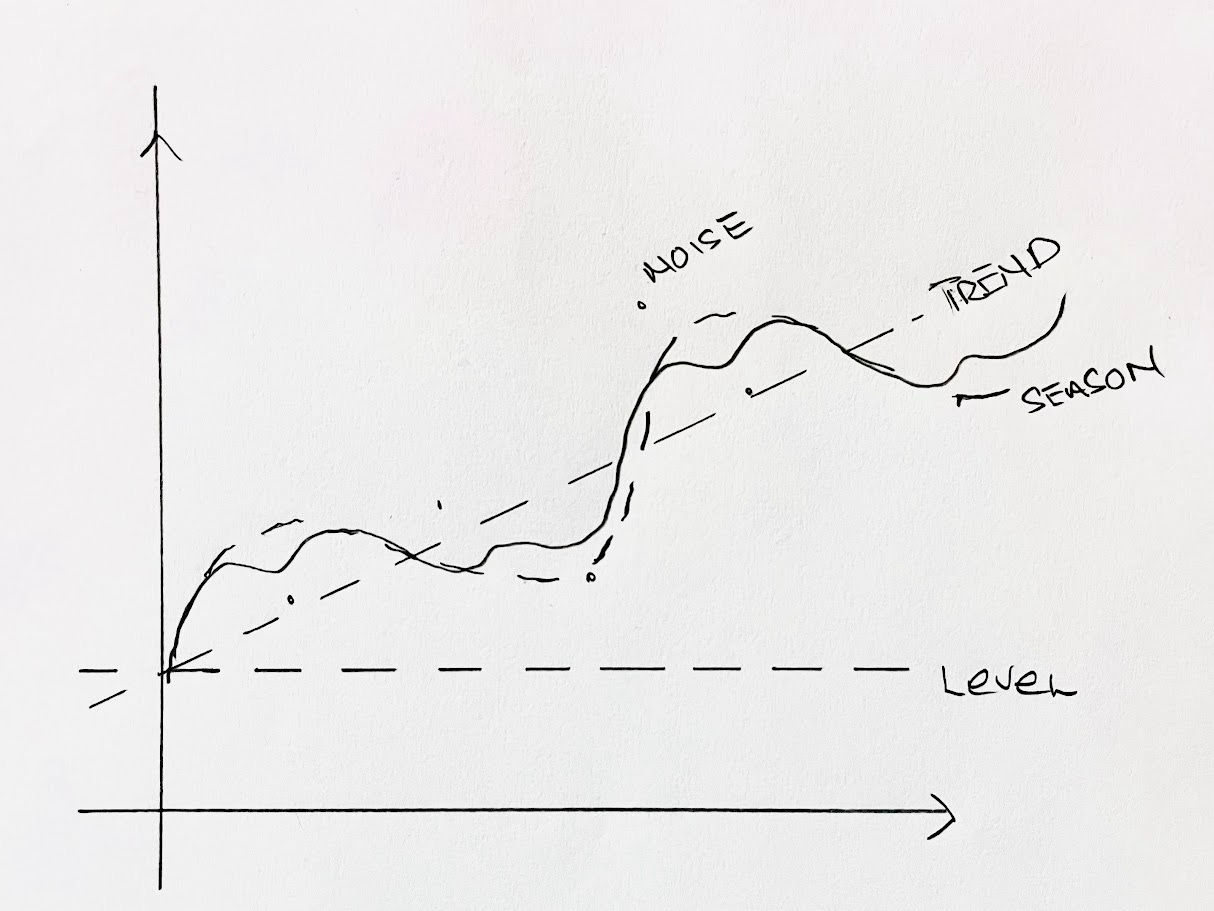
Conceptually, every time series could be understood as a combination of level, trend, seasonality, cycles and some noise.
Y = LEVEL + TREND + SEASONALITY + NOISE
Seasonal ARIMA (SARIMA) handled recurring seasonal patterns. Vector AutoRegression (VAR) tackled multiple related series. And so on and so forth.
At the M1 to M3 versions of the famous Makridakis Competition for time series forecasting, clever variations or combinations of such models were the leaders.
Aside from sequence, the other fundamental characteristic of time series that is critical is the degree of stationarity.
Much more than text or images (words only change meaning slowly over time, same for images), time series in many domains continually evolve, and are what we call non-stationary.
Recall ‘I’ for integration in ARIMA? That step leads to a differencing operation that allows the time series to be more stationary, and hence more predictable.
The classical world of time series forecasting, because of this focus on the underlying patterns of trends, seasons etc., was inherently explainable.
That’s Act I. But before I move on to Act II, I thought it would be useful to mention that forecasting is not the only task you can apply to time series. You can also nowcast (predict current unknown values with time series data to date, like GDP); classify time series patterns, detect outliers for time series, and so on and so forth. But the fundamental characteristics of time series data that need to be taken into account remain the same.
Act II: Machine and Deep Learning's Struggles with Time
The power of machine learning models in the last decade meant many tried to use machine learning models such as support vector machines, random forests, and boosting tree models for time series forecasting. But these models did not fit naturally with time series data. Not that it could not work, but it was a hit and miss.
And the natural debate then was, why switch to these significantly more complex machine learning models when the classical models were good enough?
Then came advances in computer vision and natural language processing driven by deep learning. Computer scientists being computer scientists, they started looking for new domains to test these models on. Naturally, given the importance of time series data in many commercial and financial settings, computer scientists started using these models for different tasks on time series data.
But here's the thing - you can't just throw time series data at a regular deep learning model and expect magic. Remember the importance of sequence?
Hence, sequence models for natural language processing like Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks made a lot of sense.
Answering the question of how to remember important information from way back in the sequence, while forgetting irrelevant noise applied equally to text and time series data.
There were many papers that focused on adapting RNNs, LSTMs, and even CNNs (designed for image data) to time series data. I would say the results were ambivalent. Sometimes you got fantastic results, sometimes a simple classical model would beat the complex deep learning model handily in a fraction of the time and computing power.
Even at the M4 version of the Makridakis Competition, the edge that deep learning models provided was unclear. The winner was a hybrid - a model that married classical and deep learning methods.
So was it a pointless exercise? Not really.
One of the key differences between classical and deep learning time series models was that deep learning models could utilise multimodal time series data (time series of text, audio, sensor events, images, networks), whereas classical models were largely restricted to numerical time series.
There are also many other aspects of time series that we could focus on aside from sequence for time series, distinctly different from natural language or image data.
For example:
Different time scales: Time series that change by the second, hourly, daily, weekly, quarterly and so on and so forth.
Varying signal quality: Time series data that are inherently noisier than natural language or image data.
Relationship dynamics: The importance of interactions between different time series.
There are many more. And deep learning models gave us a lot of flexibility to explore these characteristics.
In the early 2020s, even before ChatGPT, but after the seminal “Attention is All You Need” paper, many papers also explored the use of attention-based transformers for time series data.
It was a logical pairing. We use positional encodings to encode the position of tokens (or words) in transformers for text. Why couldn’t we do the same for time series steps?
I published several papers in this domain. KECE [1] combined knowledge graphs with numerical and textual time series. GLAM [2] distinguished between global and local temporal patterns with adaptive curriculum learning to handle noise. GAME [3] designed latent sequence encoders for multimodal data of different frequencies. DynMix [4] used dynamic self-supervised learning with implicit and explicit network views, while DynScan [5] learned slot concepts to handle non-stationary multimodal streams. These models showed strong results on financial forecasting, portfolio optimization, and ESG predictions, but they were highly specialized transformer models trained for specific tasks.
They were not general purpose or foundational models. Just using a transformer does not qualify! A general purpose or foundational model needs to be usable across different tasks.
But there were folks already researching these, even prior to ChatGPT coming on to the scene in 2022.
Act III: Foundation Models Learn the Language of Time
Interestingly, while I was researching multimodal time series models focused on networks, one of my PHD mates (Gerald Woo) was doing groundbreaking work on one of the first foundational models for time series data inspired by LLMs architectures.
This was the Moirai time series foundation model for universal forecasting [6]. We attended each other’s research presentations once in a while, and I found his work fascinating. But I was already at the tail end of my PHD, so too late to switch tack.
Since then there have been many more foundational models for time series data inspired by LLMs architectures.
Again, you cannot just throw a time series model into a transformer and expect some Harry Potter magic to happen.
One key challenge was how to convert infinite numerical possibilities into a finite vocabulary that transformers can process. Language has a finite vocabulary, but not time series.
Different teams solved this differently:
Amazon's Chronos [7] quantizes continuous values into 4,096 discrete bins - essentially creating a "vocabulary" for time series. Google's TimesFM [8] treats time segments as "patches" like image processing. Salesforce's MOIRAI [6] uses multiple patch sizes for different temporal frequencies. There are other such models, but the fundamental issues being solved are similar. Address the tokenisation of time series, collate a large cross domain dataset, adjust the transformer architecture to address the unique characteristics of time series data.
What’s the point of foundational models for time series?
To me, the holy grail is probably few or zero-shot forecasting. Train once on massive time series datasets, then gain the ability to perform a range of tasks - forecast sales, detect equipment anomalies, or classify patterns across entirely new domains without additional training.
Excited?
Let’s rein that in a little. The effectiveness of these as general purpose time series foundational models (akin to LLMs) is still unclear.
The key characteristics of time series data that we mentioned earlier are still key (such as sequence dependency, non-stationarity, varying frequencies, signal-to-noise ratios, and domain-specific patterns), and unlike text data, the nature of time series data in different domains (finance, healthcare, energy, retail, manufacturing, climate) can be vastly different and evolve significantly across time.
That's where we are today. Three acts, three revolutions, but the fundamental truth remains: sequence matters, patterns persist, and the future is hidden in the structure of time itself.
Why does this matter?
As with past articles in my Thinking in AI series at my Quaintitative Substack, we need to understand the data type that we are working with here - its key characteristics, it quirks - to model them effectively for our problem. And select the right tool or method for the task.
A space to watch for future acts, but I think the jury is still out on whether we will see the same shift that happened with LLMs for text.
Follow me on LinkedIn to find out more:
[1] https://dl.acm.org/doi/abs/10.1145/3490354.3494390
[2] https://dl.acm.org/doi/full/10.1145/3532858
[3] https://aclanthology.org/2022.acl-long.437/
[4] https://ieeexplore.ieee.org/abstract/document/10020722/
[5] https://dl.acm.org/doi/full/10.1145/3663674
[6] https://www.salesforce.com/blog/moirai/
[7] https://arxiv.org/abs/2403.07815
[8] https://research.google/blog/a-decoder-only-foundation-model-for-time-series-forecasting/
If you liked this AI Realist newsletter, consider becoming a paid subscriber to support this work or checking out the ai realist shop
https://airealist.myshopify.com
- Every item you buy comes with a free month of paid subscription (two items = two months, and so on).






I have a lot of data research on this. I mainly work on time perception.