On Illusion of Thinking - Do LLMs Reason?

Reviewer 3

In the past few days the paper The Illusion of Thinking: Understanding the Strengths and Limitations of Reasoning Models via the Lens of Problem Complexity hit the headlines. The paper argues that the models do not reason.

Meanwhile, the rebuttal has caused a stir, and much of the discussion now centers on whether the Apple paper still holds up. Ironically, the rebuttal is somewhat of a joke and the first author is a LLM, yet, it has received a lot of attention and has been reposted across social media as work that entirely negates the results of the Apple paper. Thus, it is worth to address the paper itself as well as the commentary.

What the original paper does:

It uses puzzles with controllable complexity to test how well models perform on reasoning tasks. The idea is: if a model can reason through simple problems, it should be able to scale that logic to more complex ones.

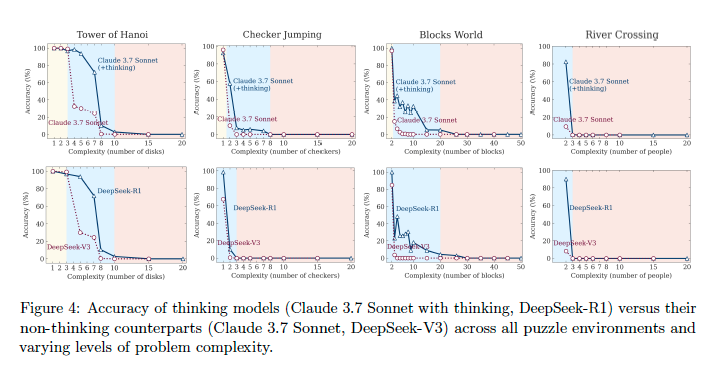
They chose four tasks to test, as shown above. The complexity is increased in a straightforward way—by adding more disks to the Tower of Hanoi, more checkers, more objects for River Crossing, and more blocks.

The logic is - if a model can easily solve a simple task, it will continue to solve more complex tasks but will use more resources. They argue that plenty of bite-size math riddles are all over the web, so a model could have just memorised the answers. If there is no reasoning, the model will just output the memorised answers but will fail on more complex unseen tasks.

As an example, they cite AIME 25 versus AIME 24 (math benchmarks from 2025 and 2024). On the newer benchmark, models score lower while humans score higher. The fact that humans do better and models do worse hints that the models rely far more on memorisation than on reasoning.

The paper has observed that as soon as the complexity increases the model starts reducing its reasoning efforts that it:

“Notably, despite operating well below their generation length limits with ample inference budget available, these models fail to take advantage of additional inference compute during the thinking phase as problems become more complex.”

This means that even though there were tokens left in the context window i.e. the model could have continued on generating the reasoning - the model did not do it and gave up even earlier than for simpler tasks.

This brings us to the commentary, which argues that the original evaluation was flawed. The commentary claims the chain of thought is shorter because the model “realised” the solution would be too long and therefore stopped generating:

“A critical observation overlooked in the original study: models actively recognize when they approach output limits. A recent replication by @scaling01 on Twitter [2] captured model outputs explicitly stating ”The pattern continues, but to avoid making this too long, I’ll stop here” when solving Tower of Hanoi problems. This demonstrates that models understand the solution pattern but choose to truncate output due to practical constraints.”

They back it up by ONE SINGLE TWEET. That is anecdotal evidence. Just one random generation that is backed up by a screenshot:

Even the person who posted the screenshot isn’t calling the original paper flawed; they’re just asking what temperature was used. A higher temperature means more randomness, so long move lists accumulate errors. That alone won’t explain the whole collapse, but it’s part of the story.:

“I don't expect this to explain all the performance drop, because, as explained in my other post, simply sampling the model can introduce errors. If each token has 99.99% probability to be correct, then the temperature 1 will eventually flip one digit and mess up runs, and that problem gets worse with higher number of disks.”

Meanwhile, the commentary based on this anecdotal evidence makes a very categoric statement:

“This mischaracterization of model behavior as ”reasoning collapse” reflects a broader issue with automated evaluation systems that fail to account for model awareness and decision-making.”

Ironically, almost no one bothered to check the references before reposting the rebuttal and claiming the Apple paper’s evaluation was flawed just because the model “stopped early” to save tokens.

Another term the original paper introduces is the wishful mnemonic “over-thinking.” This describes the phenomenon in which the model finds the right solution but keeps searching for alternative paths. As the problem becomes more complex, the trend reverses: the model first explores incorrect solutions and only later reaches the correct one. Because the model wastes the compute after it has already found a valid path, one can assume a lack of robust reasoning: it found the path but the model keeps generating purely for the sake of generating. “Over-thinking”, on the contrary, is further problematic because, although the model shows traces of self-correction, it eventually hits a limit and self-truncates its output, as discussed above.

Furthermore, the commentary brings up this formula:

It treats every move in the puzzle solution as a separate coin flip i.e. assuming each step is random. But reasoning isn’t just random path-picking until something works. Also, the authors offer no evidence for the 99.99 % per-token accuracy - they simply choose it as an “optimistic” figure. In real reasoning, once the correct pattern is found, later moves aren’t independent; the solution becomes clearer and easier as you near the end. Thus, the assumption of independence and random generation probabilities weaken this rebuttal.

River crossing puzzle

This is the paper’s biggest weakness. Once the puzzle has more than five pairs (6 pairs = 12 people or more), no solution exists with a three-seat boat, yet the evaluation still counts “no solution” as wrong. That isn’t evidence that LLMs can’t or can reason; it just shows the flaw of this benchmark.

But what is IMPORTANT - the accuracy curve already crashes at three pairs (6 people), a case that is solvable (the last graph), so the models do struggle even before the truly impossible instances appear.

Token Limit

The rebuttal argues that the observed model collapse isn’t a valid evidence of reasoning failure, claiming instead that models simply run out of context—requiring around 5 tokens per step, which quickly exhausts the available token budget. Basically, it ran out of tokens for reasoning, so it can not reason further. But this explanation is speculative at best. The original paper already demonstrates that models fail to reason correctly on complex instances, and there is no rigorous counter-evidence—just anecdotal observations on Twitter. Moreover, this line of reasoning assumes step-wise independence, as if the model must simulate every possible path in detail. In reality, when true reasoning is intact, steps are often interdependent and can be abstracted or compressed, therefore, the model shouldn’t need to enumerate them all.

“Call The Tools” Argument

Finally, the rebuttal author and its LLM resort to simply - “call the tools” argument.

The Lua-code prompt misses the point of the original paper.
It just tells the model, “Write a program that calculates the answer,” which is not what the authors set out to test. Calling an external tool (or emitting canned code) doesn’t show reasoning; the whole goal was to see whether the model could reason its way through the moves and, in principle, decide which tool to invoke on its own. Generating code here is almost certainly memorisation, the code solutions are likely to be found online (at least it cannot be excluded), so the Lua trick doesn’t address the paper’s real question.

All in all, the Apple paper still stands its grounds and the LLM-generated debunking is weak at best.